The value of pictures in mathematics

There are lots of ways of thinking about math, and some ways come more naturally to some of us than others. Some people tend to write their way to understanding; others need to hold materials in their hands, like blocks, or counters, to be able to work through a problem. And then there are those of us that are more visually oriented, where pictures become important. While we each have our own natural style of learning, pictures and diagrams can be valuable for all of us to use, no matter what our first preference might be. Drawing pictures as you learn, even if what you’re learning doesn’t at first glance seem to lend itself to pictures, has immense value for the learning process. One of the major educational benefits of using pictures in mathematics learning is that pictures provide something concrete to latch onto, allowing us to easily remember and recreate ideas and concepts when needed.

Exploring algebra visually through area models

One great example of how pictures provide strong recall is area. If you have kids that are in, or have gone through, elementary school, I bet you saw a lot of area models. An area model is a drawing that uses rectangles and area to model multiplication of numbers. Using area models is a great way to think about basic operations like multiplication, visually! But did you know area models can also help with algebra?

When students first learn algebra and the distributive law, they are at some point confronted with the following formula:

$$(a+b)^2=a^2+2ab+b^2$$

When you’re first learning algebra, this formula is easy to forget. In particular, lots of students make a simple mistake: when they see (a + b)², they want to “distribute” the exponent and rewrite this expression as a² + b², which isn’t correct. One way to help combat this mistake is to think about what this equation might mean in terms of areas. And it’s fine if you’ve never seen area models before, we can do this from scratch. The key step is to notice that (a + b)² = (a + b)(a + b) and can be interpreted visually as the area of a square of side length a + b. It’s okay that we don’t know what the values of a and b are, that won’t stop us from drawing a picture!

We start by adding two segments of lengths a and b, to make a longer segment of length a + b:

Now we make a square of this side length, and use the given lengths as a guide to cut the square into two smaller squares and two rectangles:

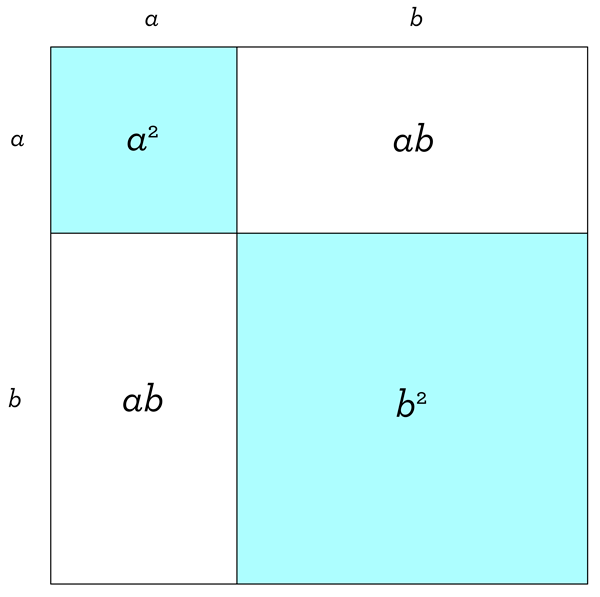
Using the familiar formula for the area of a rectangle (area equals length times width), we find the area of each of the four smaller parts of our figure (written here inside the grid for easy reference).

So what does this picture tell us? We have a square of side length a + b, which we know has area (a + b)². But we can chop it up into smaller areas: a square of area a², two rectangles each of area ab, and a square of area b². Since these smaller areas combine to give us the bigger area, we conclude that

(a+b)2=a2+ab+ab+b2=a2+2ab+b2

Pictures explain, but also help us remember

So, our picture explains why our equation is true. But even better, it tells us this:

(a+b)2≠a2+b2(a+b)2≠a2+b2

And that’s because you can see that the shaded regions representing the combined area a² + b² are only part of the entire area (a + b)², so these two expressions couldn’t possibly be equal! In other words, using this picture allows us to quickly see that (a + b)² is larger than just a² + b², and therefore not equal to it. This picture is really useful, because it helps us avoid the common algebra mistake of “distributing the exponent”. Even if you don’t remember the formula or the entire explanation that goes along with the picture, as long as you have that picture in your head, you’ll be much less likely to make that particular algebra mistake!

Next time you are helping your child solve a math problem, consider drawing a picture, even when you aren’t sure if it’s the best thing to do. Drawing pictures gives us concrete places in our memory to go back to when we’re stuck, and helps us remember things that we might not otherwise. As the saying goes, pictures are worth (way more than) 1,000 words!

Did you learn something new? Follow this blog using the links above to get other useful ideas from exSTEMsions delivered right to your inbox!

Want a chance to use pictures to help you learn math in even more ways? Check out Circles in our TpT store!