The definition of 𝜋

A recent problem is about a circular area, and when we talk about circles, that lovely number 𝜋 has a habit of appearing. But what is 𝜋? If you want to know what 𝜋 represents, you have to define it carefully, and to do that, you need a few familiar ingredients.

You may recall that the circumference of a circle is just the measure of the distance around it. In other words, if you imagine your circle is made of rope, and you cut it somewhere and straighten it out, the length of that straight line is the circumference of the circle you started with.

Also remember that any line segment with endpoints on a circle that passes through the center of the circle is called a diameter.

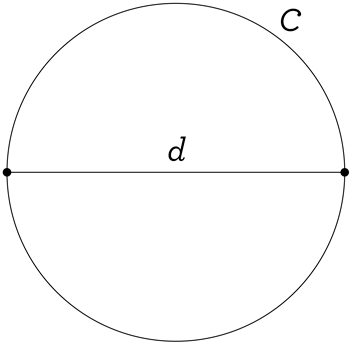
We typically name the circumference of a circle with the letter C. Since all the diameters of a circle have the same length (can you see why?), we can call that length d, and simply say that d is the “diameter of the circle”.

Now we’re ready to state the definition of 𝜋. You might remember it, and if so, congrats. But read the definition below anyway, because we want you to think about it before you read the next section of this blog.

Definition for 𝜋: The number 𝜋 is the ratio of a circle’s circumference to its diameter: $$\pi=\frac{C}{d}$$

That’s definitely the standard definition of 𝜋, and there’s nothing wrong with it. Still, read it a few times. Try to deeply understand what it’s telling you. Is there anything… missing? Any information that needs a bit of explanation?

A hidden assumption

Actually, there is a bit of information that is needed to place our definition of 𝜋 on firm footing. Our definition totally relies on our understanding of C and d. We know what these letters stand for, so no problem there. But our definition is making a bold claim, and it can actually be hard to notice: it claims that the value of C/d is always the same, no matter what circle you’re looking at. Right? That is kinda the crux of what 𝜋 is all about: draw a circle, measure C and d, get their quotient C/d, and no matter what size that circle is, that quotient is always going to throw the same number at you, that number being 𝜋. But here’s the all-important question:

How, exactly, do you KNOW that C/d IS actually the same number for all circles?

To see what we mean, draw yourself two circles of different sizes. How do you know that C/d is the same for each circle? That’s not clear at all! Why doesn’t C/d change from circle to circle? That’s a perfectly valid question! Because when you look at different circles, the values of C and d themselves change! Why would their quotient always give you the same number, for all the infinitely many sizes of circles you could possibly draw? Crazy!

Seeing the big picture

Here’s another, more conversational, way to rephrase the standard definition for 𝜋:

Since C/d is always the same value for every possible circle, let’s call that value 𝜋!

Well, as we saw above, there’s an issue here that needs to be resolved. We need to explain why it is that C/d is always the same value no matter what circle you draw! That explanation is NOT in the definition, so for the definition to truly make sense, we need that missing explanation!

Now, here’s the kicker. The explanation, really the proof, that any two circles, no matter what their size, always produce the same value for C/d, is not easy! There’s not nearly enough room in this blog to go through that proof. But that’s okay, because going through that proof is not the point of this blog. (Of course, if you’re super curious and want to know more, feel free to explore further. Or email us!)

What we want to do through this blog is to really encourage you to think hard about the definition of 𝜋. We don’t want you to do this just because 𝜋 is famous, no, not at all. We want you to do this because we want you to think deeply about everything, even the things that you were already sure of. In mathematics, surprises and subtleties abound, especially in the places where you least expect them!

Maybe 𝜋 is something you’ve thought about before. Maybe it’s something that’s vaguely familiar to you, but not much more than that. If you haven’t spent time thinking about 𝜋 before, this might be a lot to think on. Take your time with it. Think about how you might get your kids involved in the discussion. This is just the sort of magical math that kids can find fascinating, when given the chance. After all, every day is better with a little bit of 𝜋!

Did you enjoy learning about 𝜋? Follow this blog to think deeply about other aspects of math you may have just accepted before!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!