Geometry is NOT Boring

Geometry gets a bad rap
If all you’ve seen are basic facts about vertical angles and right triangles, then you might get the impression that geometry is a little… boring. Nothing could be further from the truth. Geometry can be quite lovely and fascinating, if you know where to look. One particularly interesting theme of geometry is concerned with what happens when you put geometric shapes on top of other shapes. As this might sound like gibberish, let’s see an example!
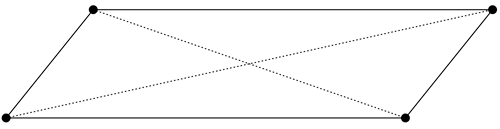
Take the lowly parallelogram. A parallelogram is a quadrilateral with opposite sides parallel:

There’s lots of things you can say about a parallelogram: its opposite sides are congruent, so are its opposite angles, etc. That’s fine, but the geometry we want to look at is much more hardcore. Let's construct a square on each side of our parallelogram, like so:
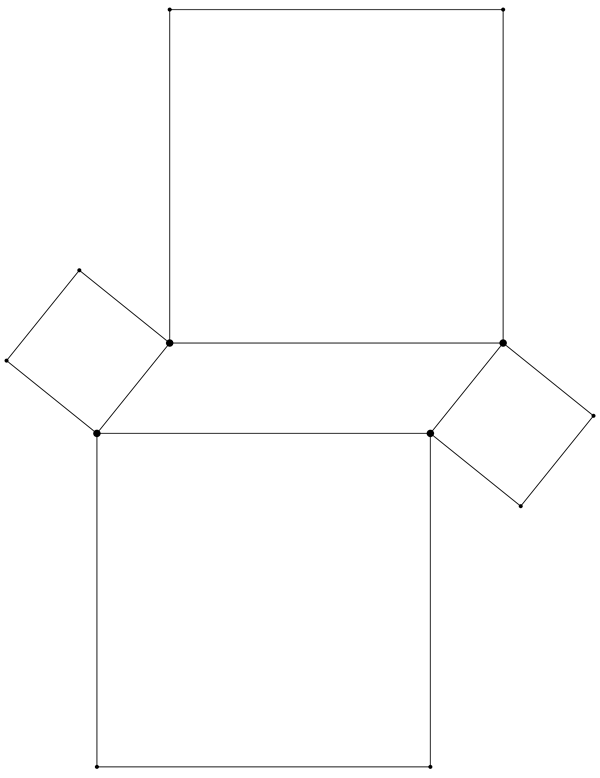
Now what? If you have a good eye and remember some terminology about squares, you can see something really cool here. Since a square is so nicely symmetrical, there is a point located at its center, appropriately known as the center of the square. As you might guess, the center of a square is right where its two diagonals intersect. For each of our four squares above, let’s draw in the two diagonals, and see where they produce the center:
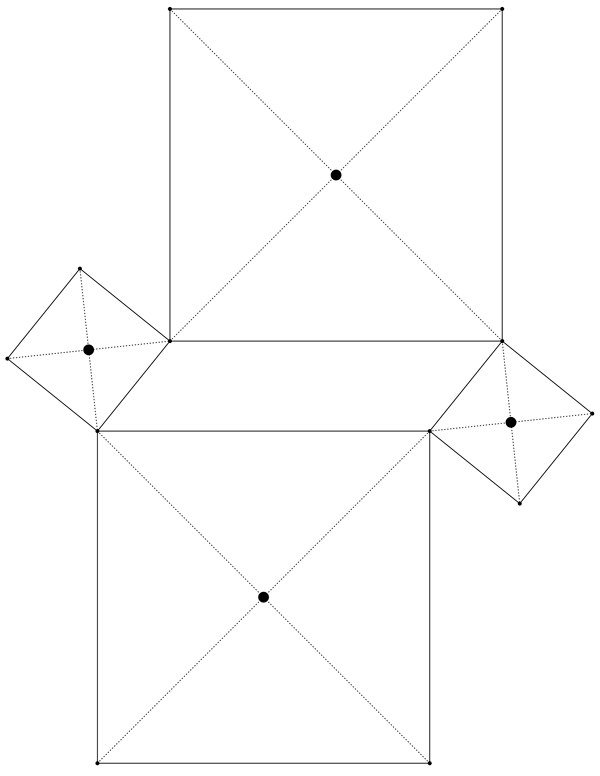
Now we can notice something very cool: the centers of these four squares form yet another square!
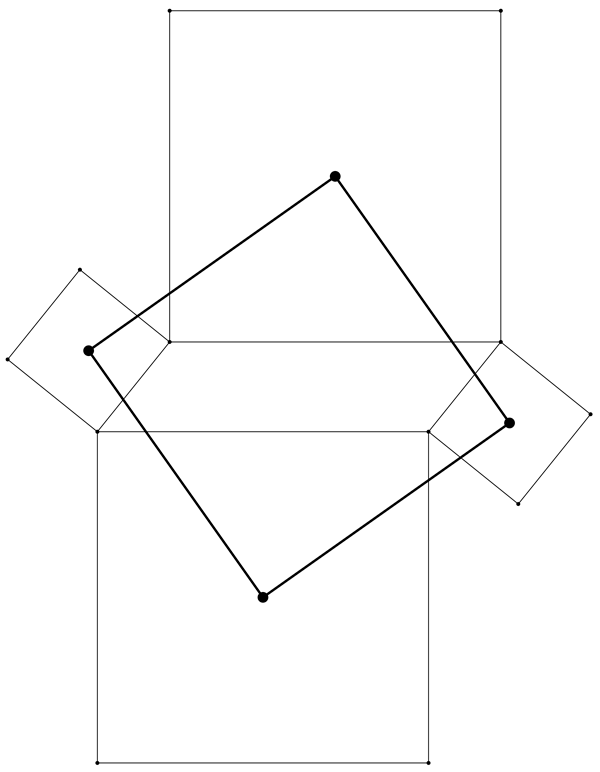
This works for whatever parallelogram you start with, no matter what it looks like! This of course needs to be proven, and we’re not going to do that here. Here, we’d just like to say… wow!
There's always another interesting question!
It doesn’t stop there; there are many other interesting questions to be asked, and we’d like to show one more of them. What we’ve done above is take a parallelogram, construct squares on its sides, and checked what was true about their centers. If we brainstorm a little bit, we might wonder what would happen if we instead constructed our squares somewhere else… what about on the diagonals of our parallelogram? Here’s our parallelogram with its diagonals drawn in:
There are only two diagonals, which might make us think there are only two squares to draw. But we had four squares above… can we get four here as well? Sure: draw two squares on each diagonal, one on each side! When we do this, we will once again be concerned about the centers of the squares, so we’ll draw those in as well:
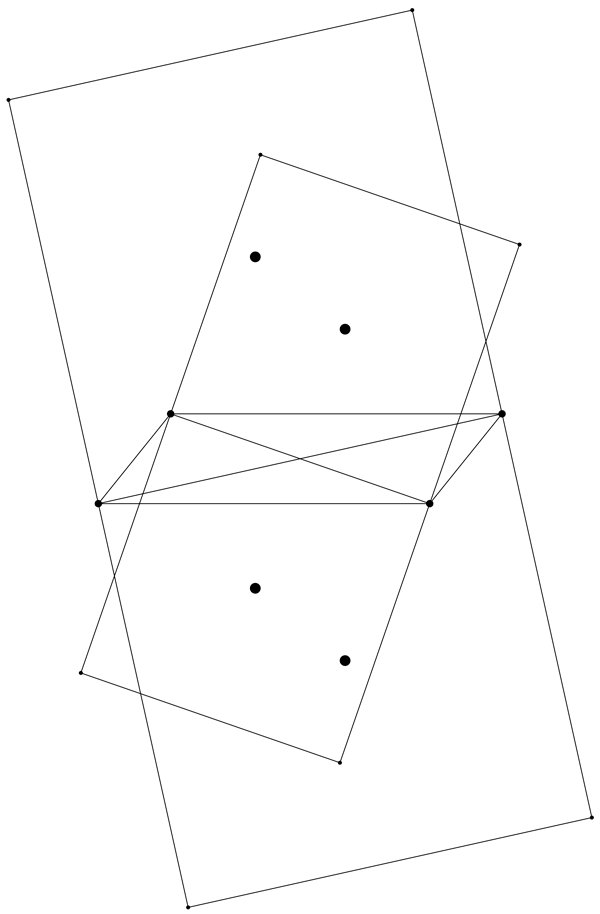
This time we didn’t draw in all the diagonals of the squares, as then this would be REALLY hard to look at, but the four big points you see are our square centers. Do you see what these centers create? It’s another parallelogram!
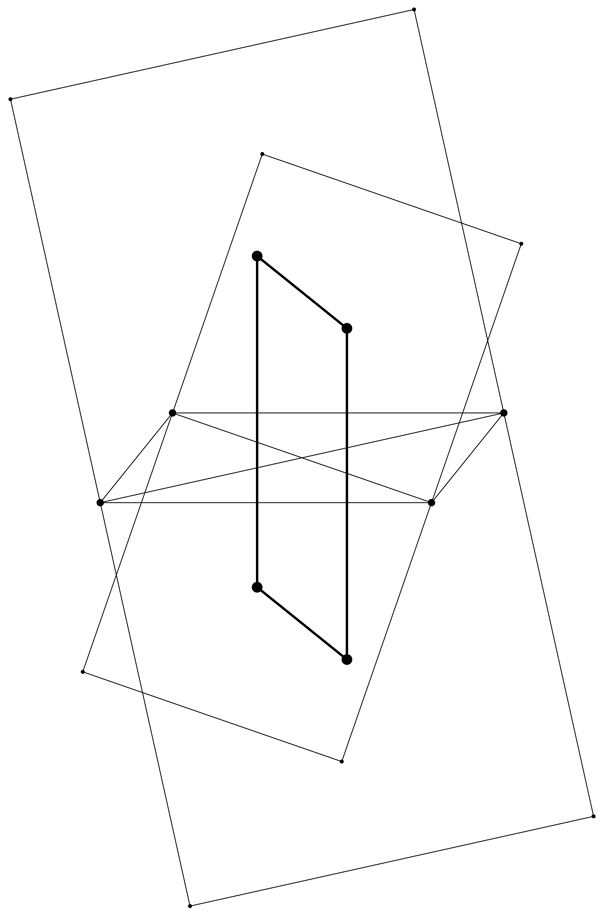
What else do you see?
If you stare at this long enough, you will notice some other surprising things. Not only do the centers of our squares form a parallelogram, this parallelogram has the same size and shape as the one we started with! And not only are these two parallelograms the same, our new parallelogram is just the old one rotated by 90 degrees! Wild! Now THIS is geometry!

Did you enjoy this post? Follow our blog (we promise, there's more than just geometry!), or use the links at the top of the page to share this post!
Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!



