A paradox has a twist ending

Do you like movies with twist endings? Or maybe you enjoy reading mysteries that completely trick you in the end? If so, then you might enjoy mathematical paradoxes. Our problem this week is a lovely paradox involving basic probability and statistics. Just when you thought you knew what was coming, the problem caught you off-guard with a totally crazy conclusion. This is the bread and butter of many paradoxes: statements that seem utterly incorrect, but turn out to be utterly true nonetheless!

Tangrams...

For example, have you ever played with tangrams? They’re really fun. The set of tangrams consists of 7 pieces: two small triangles, one medium-sized triangle, two large triangles, a square, and a strict parallelogram:

These are not just random shapes; rather, they are created in a very particular way. For example, you might notice that if you put the two small triangles together, you get a copy of that square. Although you can make them yourself, the set above can be obtained (in a bucket of many!) from various online stores. So what’s fun about them? You can put them together to make cool shapes!

...make shapes!

For example, take a look at the “bridge” shape below.

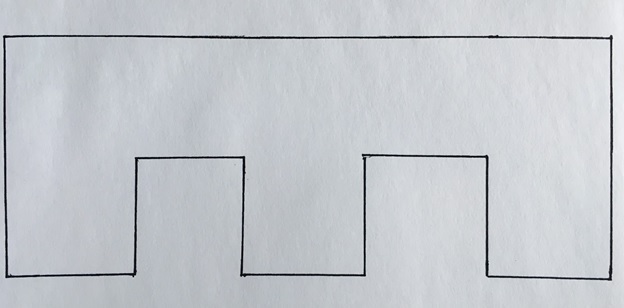
Can you form this shape from those 7 tangram pieces? (By the way, as you can probably tell, we drew this shape with a ruler and a pen. We love to be “hands on” when we work with tangrams. The playing is all part of the fun! So, please forgive us for a little sloppiness here and there. Drawing the figures and placing the pieces is actually much harder than it looks!)

Well, if you experiment for a little while, trying hard to fit all 7 pieces inside this bridge outline, you will find that you can indeed succeed:

Confronting the paradox

That’s all well and good. But now, what if we confronted you with a new shape, and again asked you to precisely form it with all 7 tangram pieces:

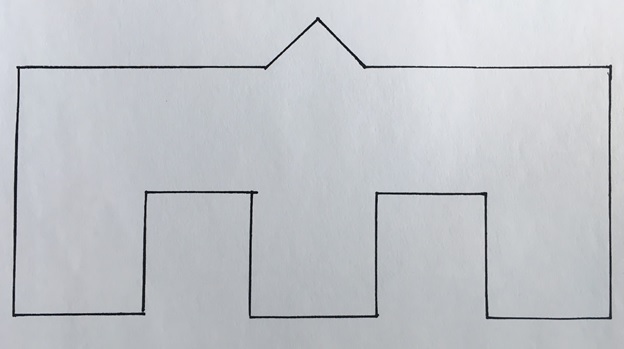
This looks like the bridge from before with an extra little “peak” at the top. There seems to be no way to construct this shape with the tangrams, right? This shape appears to have a greater area than the last, so while we could certainly fit all 7 pieces inside of it, they wouldn’t cover all of it. I mean, just compare the two pictures, yes?

Well… no. Take a look:

Huh? The same 7 pieces create both shapes, even though it seems like one shape has a greater area than the other! How can this be? Yes, indeed, how can this be?! This is an example of a “tangram paradox”. If you’re anything like me, you thought you knew what was coming, but now you’ve been blindsided by a conclusion that really seems like it shouldn’t be possible. Except it is… you can see it with your own eyes!

As for the explanation as to how this could possibly happen, well, we’ll just leave you in stitches for now. Explore it for yourself! And if you find a paradox of your own, share it with us on Facebook! And check out more tangram paradoxes in one of our upcoming problems!

Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!

Ready for MORE paradoxes? We have JUST the thing for you...try our very favorite problem-set, Paradox, from ourTpT store!