Sometimes a Jigsaw Puzzle is More than Just a Puzzle!

A simple jigsaw puzzle...
Consider the four shapes below: two squares, and two rectangles that aren’t squares:
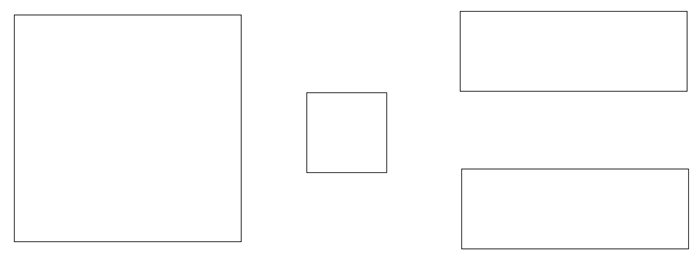
Can you put these four shapes together, like a jigsaw, to create a large square? Feel free to download them and cut them out:
And if you want to try this very quick little puzzle on your own, don’t scroll down too quickly, since the answer is down below!
...leads to some geometry...
Here’s one way of doing it:
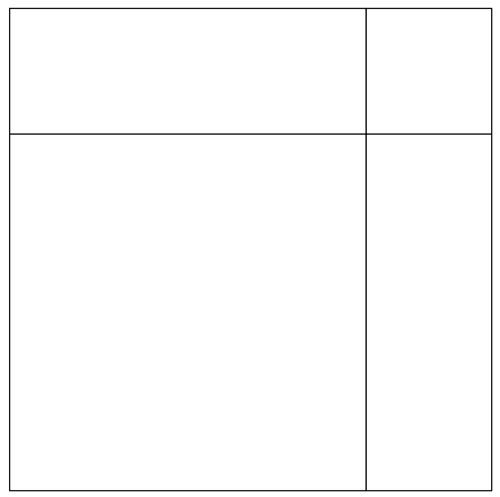
(You can also switch the position of a square with either rectangle.) Now, if that’s all there was to this jigsaw, this would be a very short blog indeed. But, we can discover some interesting ideas if we interpret this picture in a certain way. And to understand how to interpret it, we begin by asking some geometry questions.
Our first question is a very natural geometry-style question to ask: what are the lengths of the sides of our four shapes? One thing you may have noticed is that one side length of each rectangle is the same as the larger square, and the other side length of each rectangle is the same as the smaller square; that’s what allows us to complete the jigsaw! So it seems there are two very important lengths in the picture. But what are those lengths? You could certainly measure them, but what we’re going to explore here doesn’t depend on the actual lengths of those sides. We are going to treat our diagram above in the most general way possible, by saying that the side lengths of the squares are unknown; let’s call them a and b (where a is the smaller length). Let’s update our picture:
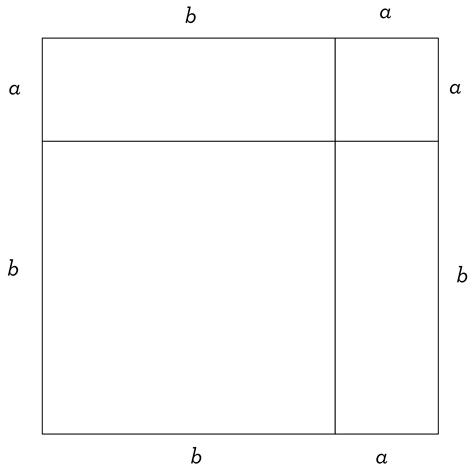
Our diagram ultimately might be very small, or very large, depending on the values of a and b; but regardless of their actual values, the diagram is always going to look like the one above, except bigger or smaller.
...which tells us something about algebra!
Our next question is also a very natural question, often asked when thinking about geometry: what is the area of our figure above? On the one hand, there’s the big picture: we’re gazing upon a large square of total side length a \(+\) b (right?). Since the area of a square is the square of its side length,
the area of the diagram \(=(a+b)^2\)
On the other hand, we could focus on the smaller details: there are four smaller shapes that make up this big square. If we find the area of each shape, and add those four areas, that’s another way of finding the area of the entire figure. So, we have a square of side length a and another of side length b: they give us areas of a2 and b2. We also have two rectangles of sides a and b, so each has area ab. Adding these areas, we see
the area of the diagram \(=a^2+b^2+ab+ab=a^2+2ab+b^2\)
We have just determined the area of this figure in two different ways. But the area of a figure, whatever number it may be, is just that one number. A shape can’t have two different areas! So if we approach an area problem in two different ways, we must get the same answer, even if those answers look different. That means that the two area expressions that we just found must be equal:
\((a+b)^2=a^2+2ab+b^2\)
What just happened here? We used area to figure out something that belongs solidly in the realm of algebra!

Algebra and identities
If you remember algebra, then you might recall that it’s all about equations, expressions involving unknowns, and identities. Algebraic “identities” are important, and in case you haven’t seen that word before, what we just found above is an example of an identity:
\((a+b)^2=a^2+2ab+b^2\)
Basically, an identity is an equation that is always true, no matter what the values of its variables. Identities are some of the tools you use when you do algebra; for instance, when you simplify expressions.
The diagram we used has an official name: it’s called a “Proof Without Words” (PWW). A picture that completely explains a mathematical concept is, literally, a proof with no words attached: you just look at the picture, think about it, and hopefully you can understand what it’s trying to tell you. Our geometry diagram is a PWW for an algebra identity. Weird, right? (And click here for another example of a cool PWW!)
Benefits and drawbacks
Having a visual explanation for a piece of mathematics can be quite illuminating. You can understand our identity by FOILing the left-hand side, of course. But you still might be missing the “aha!” moment, the click in your head that really ties concepts together. The PWW, in our opinion, serves as that click, so you can really see the why behind the FOIL. Also, that diagram sticks in your head, and once you see it, it’s really hard to forget not only what it looks like, but the reasoning behind it that gives you that identity. And, well, it’s just fun to use pictures to explain things!
On the other hand, there is one big drawback to our PWW. We know, from algebra, that our identity is true for all values of a and b. But in our picture, a and b are lengths, which automatically makes them only positive. So, we have proven our identity only for positive values of a and b. Since you also want to know that the identity is true when a and/or b are zero or negative, understanding how to FOIL using the distributive property is the right way to go, for complete understanding.
Still, there is something lovely about using a picture like this to discover something unexpected. And when you see this area explanation for an equation, you might wonder what other equations can be explained using area…. Can you find other identities that can be proven, without words, by applying geometry?
Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!
Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!
Love puzzles and want to try another kind? Check out Paradox from our TpT store!



