A magical square

In a recent problem, we ended up talking about special number grids called magic squares. We’ll have more to say about magic squares in a future blog, but right now we’d like to show you something a bit different: a grid of numbers that you can use in a mathemagical trick! Take a look at this 6-by-6 grid; each square of the grid contains a number:

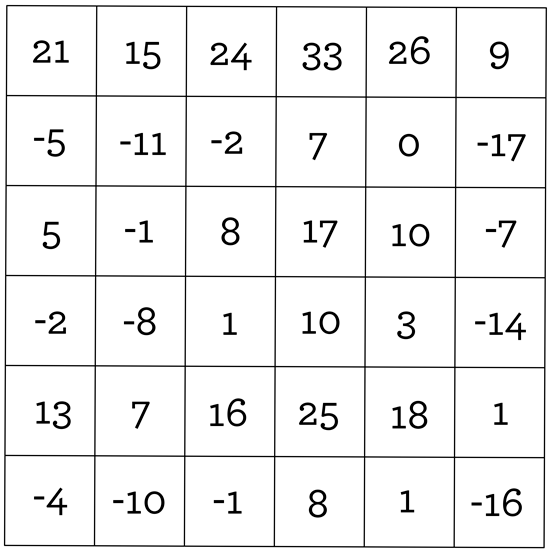
You can download a copy of this grid to print, using the button below.

So, give this grid, along with a pencil and 6 coins, to a friend. Have your friend place a coin on any square of the grid. Then, your friend should cross out all the other numbers in that coin’s row and column. Now have your friend place another coin on an available square (one that isn’t crossed out, and doesn’t already have a coin on it). Again, all the other numbers in that coin’s row and column should be crossed out (some will already be crossed out, so no need to do this again). Have your friend repeat this process with the remaining coins, until the last coin is placed in the last remaining square. Now the grid has exactly one coin in each row and each column. Here’s an example of what the grid might look like at the end of this procedure (the shaded circles represent the coins):

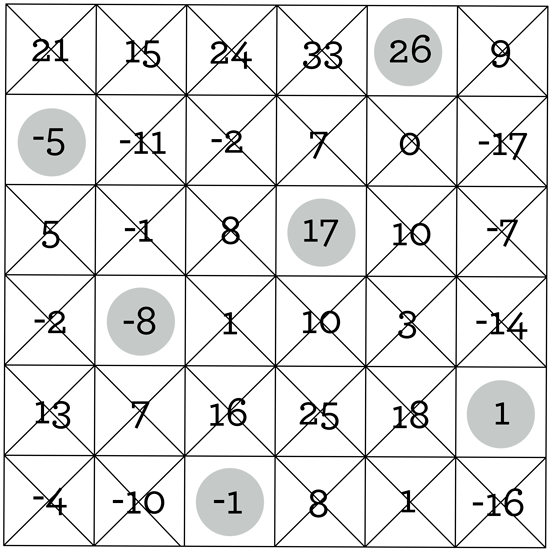
Now ask your friend to add up all the numbers underneath the coins. Here, the sum is

$$(-5)+(-8)+(-1)+17+26+1=30$$

What’s so magical about that? Well, have your friend repeat this procedure with a fresh grid. At the very end, find the sum of the numbers underneath the coins, just like before. The sum will be 30, once again. In fact, no matter where the coins end up, they will always cover numbers that add up to 30! Try it a few times yourself if you don’t believe us. So weird!

Your friend will think you spent SUCH a long time trying to create this grid. How could you possibly figure out which numbers to place in the squares, and where they should go? It seems like it would be a pretty daunting task. But actually, it’s simple. Before we explain how you can do this yourself, you might like to see if you can figure out how the trick works. If you’d like a little hint, take a look at the next diagram. When you’re ready for our explanation, read on.

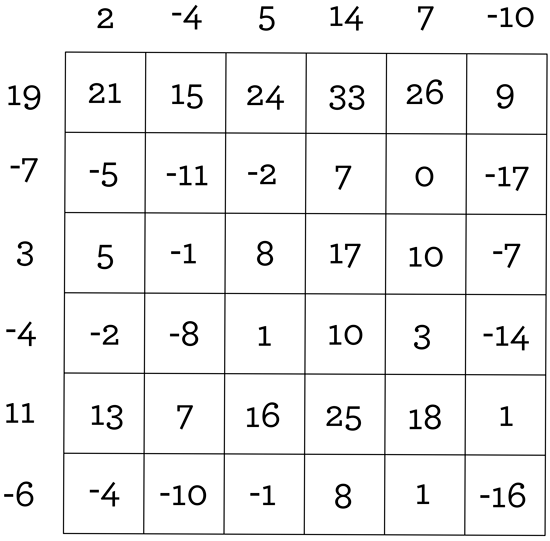
Is the square really magic?

Let’s call the numbers up top, outside the grid, the column numbers, and the numbers outside the grid over on the left, the row numbers. Every square in the grid has a corresponding row number, and a column number. Look at the numbers in the grid, and how they relate to the row and column numbers. Also, forgetting about the grid numbers for a moment, examine those row and column numbers… they don’t seem particularly strange, but we are thinking about sums here…. Hmmm….

Here’s what you might notice:

1. Each number in the grid is the sum of its row number and its column number!

2. If you add all the row and column numbers together, you get 30!

If you think about these two facts together, you’ll figure out how the trick works. Let’s go back and take a look at the numbers we placed our coins on previously, but now with the row and column numbers present as well:

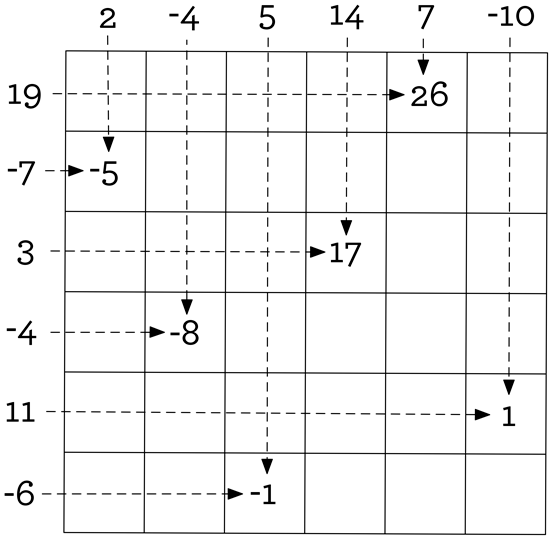
Make your own magic square

We noticed earlier that each grid number is the sum of its row and column number, as we stress using arrows in the diagram above. So, what happens when we add our “coin numbers” together? Adding up all the coin numbers is really the same thing as adding up all the row and column numbers, and we know those add up to 30! Can you see how this works, just from looking at the diagram? If not, let’s write the equation! Here’s what we get when we add our coin numbers:

$$(-5)+(-8)+(-1)+17+26+1$$$$=(-7+2)+(-4+(-4))+(-6+5)+(3+14)+(19+7)+(11+(-10))$$$$=-7+2+(-4)+(-4)+(-6)+5+3+14+19+7+11+(-10)=30$$

Since the coin placement guarantees exactly one coin per column, and exactly one coin per row, adding all the coin numbers really just adds up all the row and column numbers, two at a time! Nice.

Now, why not make your own grid? Pick your favorite number. Experiment a little bit, and find 12 numbers that add up to your favorite number. Choose 6 of these numbers to be the column numbers, and the other 6 will be the row numbers. Now you’re ready to make your magic grid: for each square in the grid, write in the sum of that square’s row number and column number. (When you’re ready to spring this trick on someone, make sure that you keep your row and column numbers to yourself, otherwise you might give away the secret.) When you ask your friend to place the coins, those coin numbers are guaranteed to add up to your favorite number!

By the way, you can use any size square grid; start off with something smaller until you get the hang of it. If negative numbers are bugging you, feel free to use only positive numbers. And hey, nothing’s stopping you from using fractions and decimals in your row and column numbers!

Go beyond the magic square

There are also some other puzzling things to think about here. For example, look back at the grid numbers again; do you notice how sometimes a number and its negative seem to appear with another number and its negative? Take a look at \(-\)1 and 1, appearing next to \(-\)8 and 8. And how about 17 and \(-\)17, with 7 and \(-\)7 close by? Can you find another example of this strange occurrence in the grid? What’s going on?

There’s always more math that can extend your thinking. Our unique problems help you go a little further, every week! You can try your first two problems for free with our 2-week free trial. Sign up here!

If you and your kids love this puzzle, and want to try another that's equally awesome, yet totally different, check out our tangram paradox puzzles!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!