What is Graph Theory, and Why Does it Matter SO Much?
A “graph” isn't necessarily a chart or plot!
To solve a recent problem, we drew pictures to help us organize our thinking and guide us to the solution. These pictures looked like connect-the-dots puzzles, where dots are connected to other dots with lines, like this:
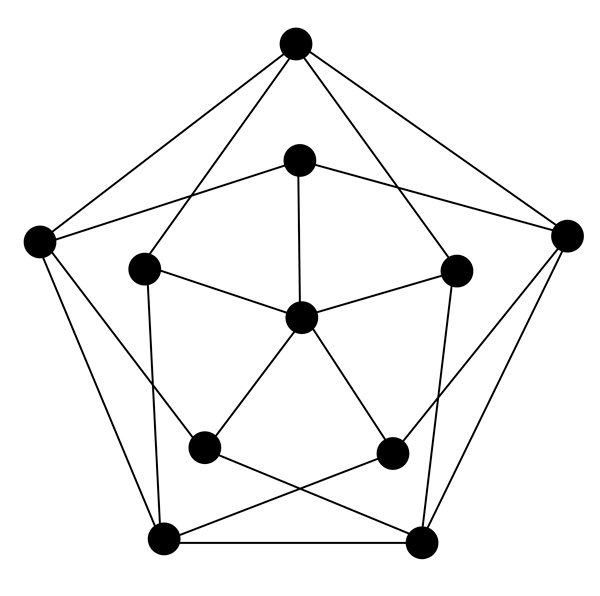
Such connect-the-dot structures are called graphs. They may not seem like anything useful that you could apply to the real world, but if you surf the web, use apps on your phone to help you arrive at a destination, or access social media, then graph theory is there, lurking beneath the surface! Let’s see how.
(And just to clarify, here the word “graph” does not refer to any pictures you may be familiar with from statistics, like pie charts. Even worse, “graph” doesn’t refer to the picture you get when you plot a function on the coordinate plane, which is one of the most common usages of the word! The meaning of the word depends on where you’re at in mathematics; unfortunately, this can be confusing!)
The dots of a graph are called vertices (and the singular of that word is vertex), and the lines are called edges. Graph theory is, of course, the study of graphs. (And, by the way, that graph above is fairly well-known to graph theorists. It even has a name: the Grötzsch graph!) There are many things one could study about graphs, as you will see, since we will encounter graphs again and again in our problem sets.
For now, we’re just content to ask a very natural question: why would anybody study graphs? I loved connect-the-dots puzzles when I was a child, but I never would have guessed that there is anything useful about them. But graphs are actually very useful, and not just in various fields of mathematics. Graphs are useful out here, in the real world!

Real-world applications of graph theory
The usefulness of graphs lies in their ability to model many different situations. In our problem, we drew graphs where the vertices represented people and the edges represented friendships. We talked about imagining actually walking on a graph. So, why not go further: the vertices of a graph could represent towns, and the edges the roads connecting them! So graphs are a really handy way of representing road maps. And if you imagine a graph where vertices are cities and edges are roads, you might immediately be interested in the shortest distance between two cities, if you have to travel from one city to the other. If you’re anything like me, you are asking your phone app exactly this question several times a month! As graphs can be used to model maps, and there are plenty of apps on your phone showing you how to travel from city to city, you can bet that graph theory lies behind much of the mathematics that produced those directions that you’re following!
A roadmap is an example of a network. A network is just a bunch of interconnected objects. In a roadmap, our objects are cities, and they are connected by roads. If you have a network of things connected to other things, this network can be nicely visualized by using a graph. The things in your network can be represented as vertices, and the connections represented by edges. And if a graph can model a network, then graphs can model all sorts of important things! For example, the internet is a network! If you think of websites as vertices, and edges telling you which websites are linked to which others, then the World Wide Web is really just a gigantic graph! How about Facebook? Friendships on Facebook can be easily modeled by graphs: each person is a vertex, and an edge connects two people if they are friends. Researchers study social media for all kinds of reasons, and graph theory is behind much of that research. And don’t think for a second that Facebook isn’t also using graph theory to study the interactions of you and your friends!
Since networks are everywhere, graph theory is everywhere, too. Graph theory is used to model and study all kinds of things that affect our daily lives: from transatlantic shipping routes to integrated circuits, from molecular bonds to animal food webs. Who would’ve thought that connect-the-dots would be so important to our world?
Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!
Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!
If you'd like to try a graph theory problem, head to our Teachers Pay Teachers store, and check out Volunteers!



