Building Your Child's Problem Solving Tools: Drawing

Solving problems by drawing
This blog is the first of an occasional series on problem-solving techniques. One technique that often comes in handy when solving a problem is drawing pictures. Pictures serve many purposes: for one, they can help you keep track of information that would be difficult to process otherwise. Pictures can help you see concepts from a different perspective, giving you ideas on how to proceed in a problem. Pictures generally facilitate playing, brainstorming, and “risk-taking”: daring to have fun with the mathematics, letting things fall where they may, and hopefully gaining some insight into the solution in the process.
The playing part of drawing pictures is the focus of what we will call “naive drawing”. You don’t have to know exactly what you’re doing, or where you should end up, when you create diagrams to help solve a problem. You can be “naive”, just doodling whatever comes to mind; the things you draw should have some vague connection to the problem, but don’t worry about whether your pictures are immediately helpful or recognizable, or not... just draw! Rather than planning out each and every step, you can “improv”, and see what you stumble upon. You might just accidentally come across the key idea that solves the problem!
A strange and lovely geometry problem
Let’s take an example. We love lovely problems, and here is one:
Before you lies a flat sheet of paper, infinite in extent in all directions… in other words, a plane. You have two crayons, one red, and one blue. You decide to color each point in the plane one of these two colors. Explain why, once you are done, you are guaranteed to have two points exactly 1000 miles apart!
This seems to be some sort of geometry problem, so drawing pictures might be helpful, no surprise there. But which pictures? You could draw your plane as a big rectangle, but if you have a piece of paper in front of you, you are staring at a part of that plane already, and pretending that you’ve colored every point either red or blue. So, how could you possibly guarantee that either two red points, or two blue points, are 1000 miles apart, no matter how the points are colored? For lack of anything better to do, let’s start imagining different objects that might be living on that plane, in your paper. There are all sorts of geometric figures residing in your plane: line segments, triangles, and quadrilaterals, just to name a few. Since you’ve just colored every point in the plane as red or blue, the objects that you imagine are also colored, since these objects are made of those points. So, when you experiment by drawing shapes on your paper, you should think of these objects as having each of their points colored either red or blue. As you draw these objects, you are teasing them out of their hiding places, and thinking about how you can use them, and all their blue or red points, to your advantage.
Now, there are a few ways of getting to the solution, but it turns out that there is a very simple picture that is key to understanding what’s going on here. Before reading on, draw some pictures! Don’t overthink it. Perhaps you see the answer immediately; if so, rock on! If not, no worries; just draw.
Just draw something, anything!
You might now be thinking, “what can I draw, if I don’t even know how to start? Being naive is one thing, but the only thing I’m drawing right now is a blank!” Here’s one way you can start: reread the problem. We are interested in a very special distance: 1000 miles. Draw that. It doesn’t seem like much, but do it (on a much smaller scale, of course!).
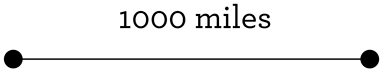
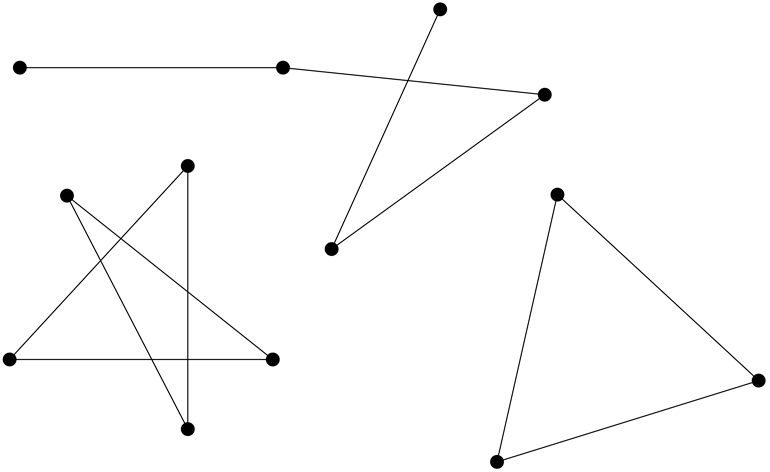
So? Now what? Well, what if we put several of those line segments together? If you have segments of that particular length in mind, what can you create with them? What kind of figures can you draw? For example, you might draw a square. You might also draw a star shape, with segments shooting off a common point.
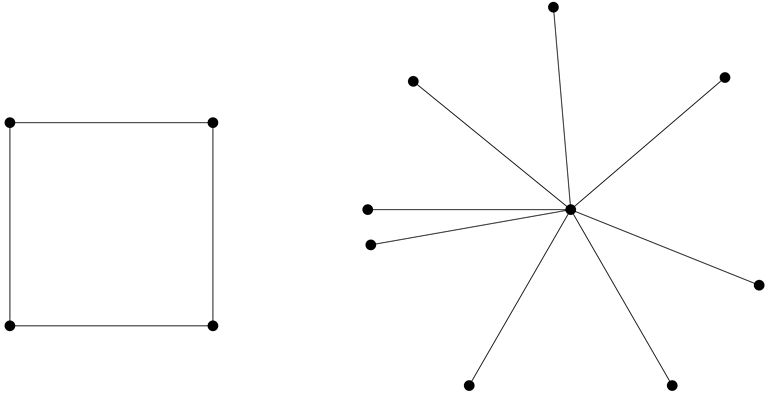
Keep in mind, now, we are playing, but we are also trying to understand something very specific: why must we have two red points or two blue points 1000 miles apart? Somehow, no matter how we color the points of the plane, we have to convince ourselves that we will always see two red points, or two blue points, somewhere, that are the endpoints of a segment with length 1000 miles. Do our pictures help us here? How could our pictures help us? What if we drew a picture that somehow forced two points of the same color 1000 miles apart? In other words, can we draw a picture that dooms us to have two endpoints of the same segment with the same color, no matter how we color the endpoints? If we can find such a picture, we would have our solution.
Focus on the drawing
So, let’s focus our thinking on the particular diagrams we are drawing. Again, our new question is: can we find a picture, where no matter how we color the endpoints of our segments, we must always see two endpoints of the same segment that have the same color? For example, take our square, and imagine that the sides of the square have length 1000 miles. We could color the vertices of the square all red, or all blue, and then we’d certainly have endpoints of the same color 1000 miles apart. But that doesn’t have to happen. We could color them like so, avoiding endpoints of the same color:
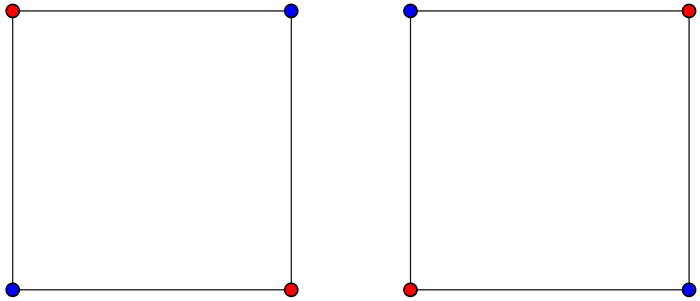
What about our star shapes, where all segments are 1000 miles long? Do they force us to have endpoints of the same segment with the same color? Unfortunately, no:
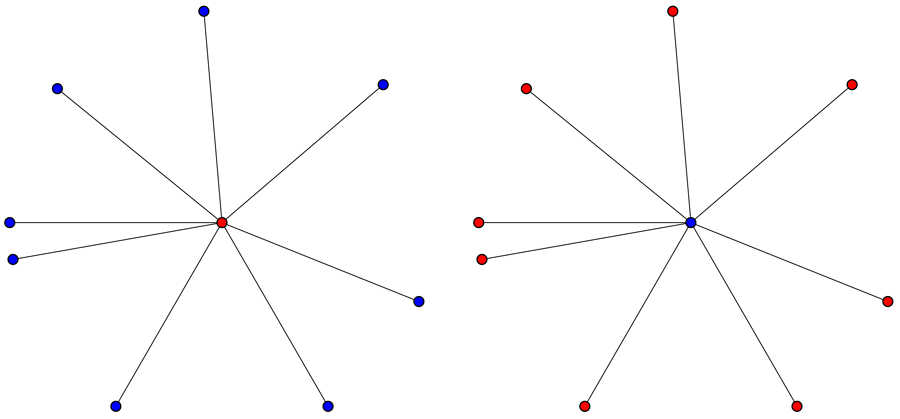
So, a few failures, but never fear! We’ve understood a little bit more. Keep drawing!
You may have drawn something helpful somewhere. Experiment, and consider each picture you draw to see if it tells you anything interesting. Maybe you don’t have to get too complicated? Since you drew a square, you might draw a nice equilateral triangle, as we did above:
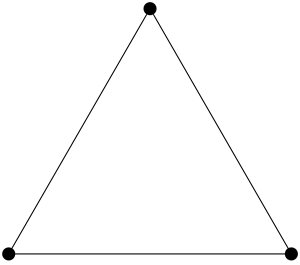
Now let’s check it; how can we color the endpoints of its sides? Here are all the ways to do it with our two colors:
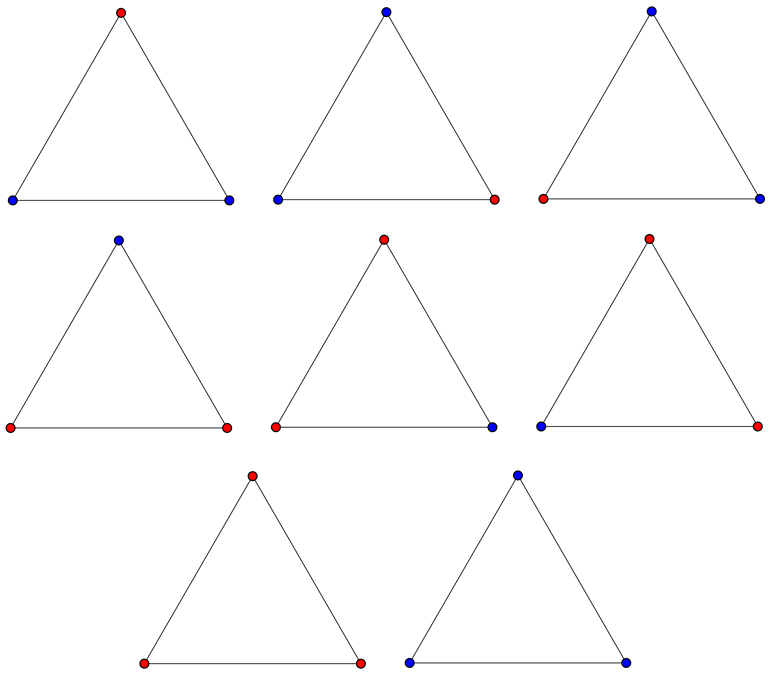
Well look at that! No matter how you color the vertices of an equilateral triangle, there will always be two endpoints that have the same color! But wait, that solves our problem, doesn’t it? Because we’re thinking this is actually a triangle with sides that are 1000 miles long!!

Time for a recap. We found a special figure in the plane, an equilateral triangle of side length 1000 miles. Wherever it might be situated, we know something about its 3 vertices: if you color those 3 points red or blue, you can’t avoid two endpoints of the same segment that are both the same color. And that means no matter how you color the plane, since this equilateral triangle is sitting inside of it, you must have two points somewhere of the same color that are exactly 1000 miles apart! Cool!
Extend thinking beyond the drawing
These are the kinds of problems we like here at exSTEMsions. Weird, exciting, and instructive. By the way, we can extend our thinking by noticing that this solution gives us more than what we bargained for: there are actually infinitely many pairs of points in the plane that are the same color and exactly 1000 miles apart! That’s because the plane is infinite in extent, and there are infinitely many equilateral triangles in this plane! Every one of those triangles will have a pair of same colored endpoints. Even cooler!
And, we can extend our thinking even further, not by noticing something else important, but rather by noticing something that isn’t important. Namely, the number 1000, and the unit (miles), are nothing special. We didn’t use this information at all in the solution! Sure, we talked about them, but we didn’t rely on them. For instance, if we wanted to understand why there are two points of the same color that are only 5 centimeters apart, then we would go through the same steps as before, and again arrive at our desired conclusion. So, this solution works just as well for any distance, and any unit! Think about it! Even cooler!
So, have fun, and be naive in your drawing. It can lead to wisdom!
(And here’s an extra credit for our subscribers: how can you apply the principle we learned in this week’s Problem to make the solution to our blog problem incredibly quick to write down?)
Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!
Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!



