A Discrete Geometry Drawing Challenge

What is discrete geometry?
A recent problem was all about something called discrete geometry. What this kind of geometry deals with is actually a little hard to nail down quickly in a down-to-earth blog, but we can give you an idea: it’s the part of geometry that deals with discrete things! And what does that mean? Well, if objects are discrete, you can think of them as completely separate from each other, almost like each object comes in its own separate bin. In particular, you could count these objects if you wanted to. Now how does this differ from the typical geometry you may have learned at school? Well, what if I asked you to count the number of points on a line? You would tell me that the number of points on a line is infinite, but there you didn’t really count anything, you just knew that basic fact about points and lines. But there are plenty of problems (like this week’s) that demand you actually count points, lines, regions, all sorts of geometric things, kinda like how you would count marbles in a jar. Here’s an example of such a problem; not only is it a fun drawing exercise, it provides a teachable moment about something rather unexpected, as you’ll see. By the way, as we go we're going to be asking you to try to draw some interesting things. We've included drawings of our own, so if you'd rather not spoil the fun, scroll carefully….
Drawing chords, and counting regions
So, we start with a circle of any size. What we’re going to do is start drawing chords on this circle. A chord is just a line segment that has both endpoints on the circle, like so:
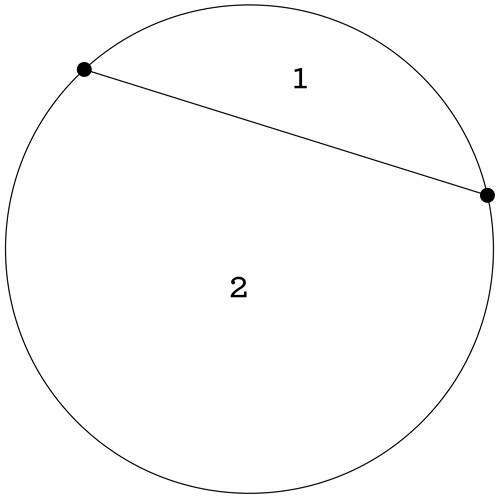
Notice that when you mark two points on a circle and draw the chord between them, you have split the circular region you once had into two smaller regions. We have counted them in the picture. Now where do we go with this? Well, what if you started over and marked 3 points on your circle? How many regions can you make by drawing chords between your points? In other words, what’s the greatest number of regions you can make? Or, in other other words, if your circle is a pizza, and you don’t mind slices with crazy shapes, what’s the largest number of slices you can make with straight cuts, always starting and stopping at your chosen points? Here you go, for 3 points:
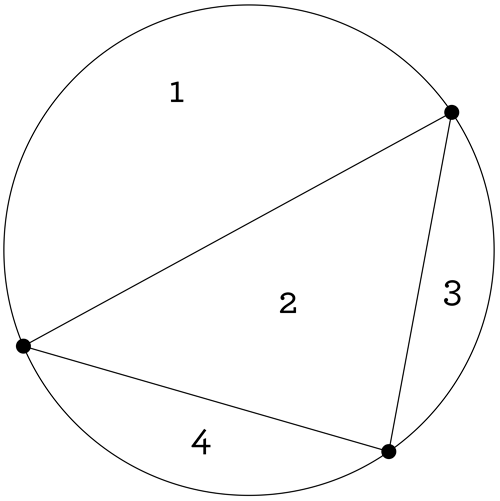
Notice that to make all the possible regions, you need to draw all the possible chords (to get the most slices of pizza, you have to make every possible cut). Above, regardless of where you place your 3 points, you will find that you have created 4 regions. So, next: what’s the greatest number of regions you can get by drawing chords between 4 points? Try it yourself, then take a look at our drawing and compare it to yours.
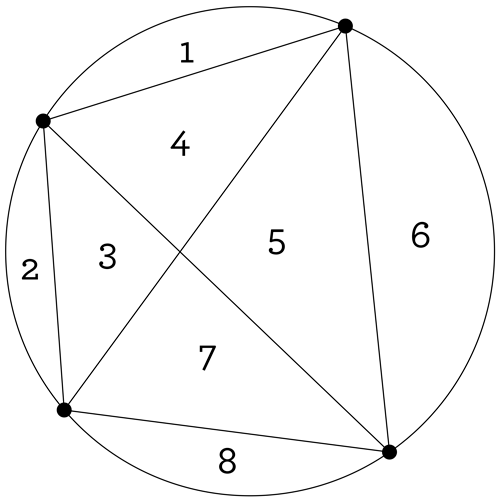
So, 8 regions. Now, trust us, something amazing is going to happen if you keep playing along with this. Try drawing the picture for 5 points. Draw all the possible chords between your 5 points, so you get the maximum possible number of regions. When you’re ready, take a look at what we’ve drawn, and compare the two.
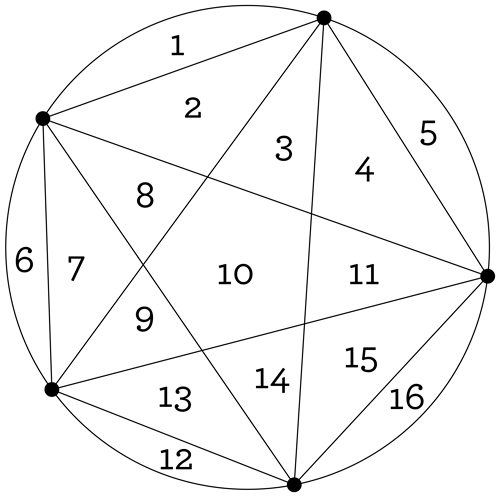
Are you seeing a pattern form with the numbers of regions we’re getting? Let’s put our meager results in a table, to see what’s what:
| Number of points marked on the circle | Greatest possible number of regions you can get by drawing chords |
|---|---|
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
Is there a pattern?
The pattern seems clear: the greatest number of regions you get when you add another point to the picture is just twice the number of regions you had before. So, for 6 points on the circle, we should get 32 regions? Try it. No, really, please? We swear this is going to be fun. Just draw things VERY CAREFULLY (you have been using a ruler, we hope!). When you’re satisfied with what you’ve drawn, check out what we have to see how they compare.
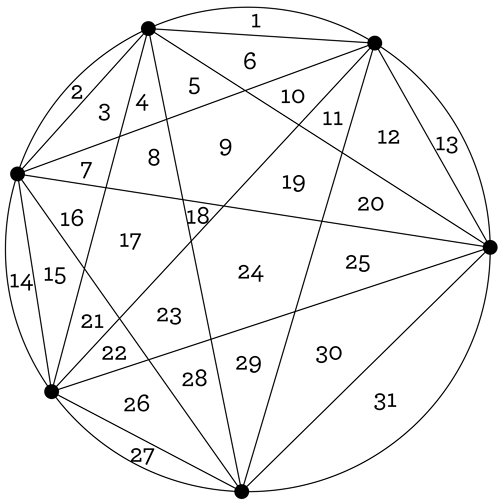
That’s right… the greatest number of regions you can get, starting with 6 points and drawing all the possible chords, is only 31!!! IT ISN’T 32. Think about that. Wow!

In case you missed a region...
By the way, did you get 30 regions in your drawing for 6 points? If you did, then you may have ended up drawing a triplet of chords like this:
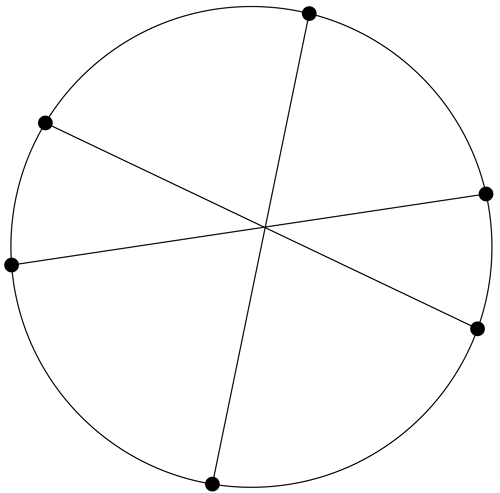
If you place your points so that 3 chords all cross each other at the same place, you will miss a region you should’ve gotten! To see why, in the picture above, let’s move one of the points a little bit; say, the top one, shifted off to the left:
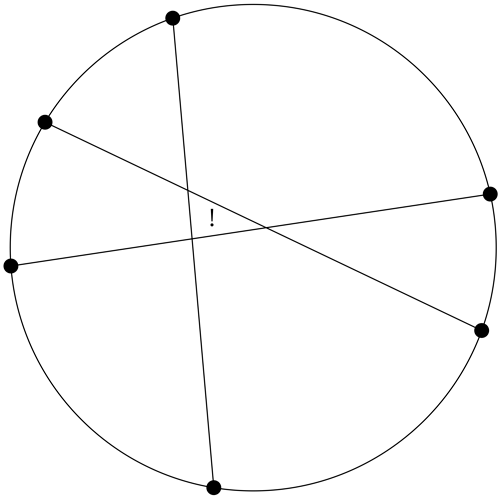
Ah, look! Another region popped up! So, since we’re looking for the maximum number of regions we could possibly get, we have to be a little careful: we can’t allow three chords to all pass through the same spot, since that destroys an extra region we could’ve had otherwise! If that happens to you, no problem, just erase one of the offending chords and shift one of its former endpoints to the left or right. Draw that missing chord back in, and you’ll have an extra region.
The pattern failed!?
Anyways, let’s get back to the main issue here. That supposed pattern we saw? It’s broken!!
| Number of points marked on the circle | Greatest possible number of regions you can get by drawing chords |
|---|---|
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
| 6 | 31 |
Very cool, and very surprising! Patterns don’t always work out the way we think they will (which also happens in this week’s Problem!). We assumed that we would get 32 regions because, well, every time we spotted a pattern in our math classes, it worked out just fine. And that’s because when you learn math, the problems are specially chosen to be “nice”. But not every problem plays nice, and really that’s wonderful, since then wild things might just jump out to entertain you!
The next question is: why does the pattern fail? We don’t have room in this blog for that answer; we can tell you that it depends on some basic counting methods in discrete math, including something called a binomial coefficient. Interested? Try exploring on your own, or reach out and ask us whatever questions you might have on Facebook or Instagram!
Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!
Looking for other drawing challenges for your family to try? Download Circles from our TpT store!



